Illuminated Knits now available in print!

I'm delighted to announce that print copies of Illuminated Knits are now available to pre-order!

The book contains four patterns (the Iona blanket, the Lindisfarne shawl, the Durrow shawl and the recently released Kells pullover). There's also a short introduction where I discuss my sources of inspiration, a general guide to slipped stitch cabling and also a bit of advice on how best to choose colour combinations.

The book also includes a full stitch key, and some hand-drawn sketches of the main cable patterns which can be coloured in to help experiment with different colour combinations - these can both be downloaded for free as PDFs on this page (scroll down to 'Additional Materials' at the bottom of the page)

If you already have the e-book collection of Illuminated Knits on Ravelry, you will shortly receive an update that includes the digital version of the finished print book.

I'll be in Inverness at Loch Ness Knit Fest from Fri 13th Oct to Sun 15th Oct - I'm currently waiting on a delivery confirmation but it looks like I should have some copies of the book available to sell at the festival. Just for fun, I've also made up some printed cards with sketches of the cables to colour in - the first 20 copies sold via my site will each receive a set free!

We're currently planning a proper book launch to take place at Kathy's Knits in Edinburgh - more details to come very soon!

Durrow shawl

It's been a while in the making, but I'm pleased to announce the third design in the Illuminated Knits collection is finally here - the Durrow shawl!

This design took several months to conceptualise and bring into reality. I think it might be fair to say that it's the most complex design I've ever created - both in terms of the cable pattern itself, and the knitting required to achieve it. I'm very happy with the end result though, and glad that I persevered even when it was completely refusing to make sense!

In keeping with the other designs in the Illuminated Knits collection, Durrow uses a technique of cables mixed with slip stitches to create a contrast colour design - I love this technique, because it gives you the chance to play around with different colours without actually having to use stranded knitting or intarsia. The colour-work is as simple as striping the colours on each round, and remembering to slip stitches when necessary (like mosaic knitting). This is the technique that I also used in the Iona blanket and Lindisfarne shawl.

One slightly finicky thing about this technique is that it does draw the fabric in a little bit (vertically, because of the slipped stitches), and so the fabric becomes much denser as a result. Because cable knitting also a tendency to do this (particularly the type of complex cables I use, where the rate of horizontal travel can be quite extreme), I decided to only use this technique when working in the round. Why? Because when you work in the round, you can change colours on every round, so the contrasting stitches only need to be slipped over one round. When you use this technique whilst knitting flat, you can only really change colours every 2 rows (so that your yarn ends up in the right place to strand up the side), so the contrasting stitches have to be slipped over 2 rows instead - creating even more pull-in and a denser fabric (there are ways of getting around this, so that you can knit flat whilst changing colours on every row, instead of every other row - however this is a bit complicated to describe and not something I wanted to do throughout an entire design; I have used it a little bit in this pattern though... more on that in a bit!).

So, with these constraints in mind, I began to think about how I could use this slipped stitch colour technique in a triangular shawl. It is possible to knit a triangle shape entirely in the round (if from the centre out, for example. by concentrating increases at three evenly spaced points on each round); however, this will produce something more like an equilateral triangle, not the right-angled shape more commonly made (and worn!) by knitters. After a lot of head-scratching, I realised that this problem could be solved by making a border out of modular squares (which can be knitted in the round), with picked up stitches for the body (which can be knitted flat, and shaped like a traditional right-angled triangular shawl).

Here are some of my notebook sketches that show my efforts to work out a suitable square knot for the border (I wanted to use two different coloured cable strands, so I was trying to figure out one knot that could flow across the entire border, and then another self-contained background knot that only occurs once in each square):

I realised that I could make the cable pattern flow all the way across the border if I alternated centre-out and centre-in squares. This helps to avoid the half-stitch jog (illustrated by Joni Coniglio) that will occur if you try to graft/pick up and knit stitches from pieces of knitting where the direction of knitting is opposite. Alternating centre-out and centre-in means that the direction of knitting across the squares, at the edges, is always maintained and so the cable flow perfectly. This picture probably shows it more clearly than I can describe:

The squares on the far left and far right are both knitted centre-out; then the live stitches at the edges have been used, along with 2 provisional cast-ons, to start the middle square which is knitted from the outside to the centre. If you look closely at the edges of the middle square, you should be able to see how the main cable (in turquoise) flows seamlessly across all of the squares.

Also, you can see in the above photo how I've used slightly different colours for the background yarn of each square; this creates a nice gradient-type effect, and is one of the fun possibilities that arises from working the border in a series of modular squares. However, I think the border would also look lovely with only one background colour (the main reason I used three was simply because I couldn't choose between them!).

This construction schematic shows the order of centre-out and centre-in squares, with the arrows showing the direction of knitting:

You may remember earlier, when I was describing the problem with using this slipped stitch technique whilst knitting flat... well, I ran into this problem when trying to design knots for the corners (the corners are the bits at either end of the border, shown in both the above and the following schematics):

I decided to only continue the main cable pattern to the corners, and drop the self-contained background cable (a sacrifice to try to keep the level of complexity down! It would have been possible to include the background cable too, but I tried knitting it myself and nearly tore my hair out, so I figured other knitters might also find it a bit frustrating). The difficulty arises because these corners need to be knitted flat (you start from the outside and work decreases inwards to make the right-angle triangle shape, rather like the body of the shawl but in miniature). So, to get the working yarn to end up in the right place so that you can change colour every row (instead of every 2 rows), you need to work 2 RS rows followed by 2 WS rows. This makes some WS cables necessary, but I was able to write the pattern in such a way that these are kept to a minimum.

After the border has been knitted, and the body picked up along the edges and worked upwards with decreases towards the neck edge, the top edge is finished with an i-cord cast-off and the outer border edge is finished with a lace edging (both visible in the above photo).

After spending so long on perfecting the design of this shawl, I felt a sense of melancholy (mixed with a bit of relief!) when I cast off the last stitch. It always feels a bit strange to finish such a large and complex project, but I'm looking forward to diving into my next (and final) Illuminated Knits design.

I will be exhibiting the sample of Durrow (along with most of my other knitted samples!) at the upcoming Edinburgh Yarn Festival (March 10th and 11th). I'll be at stand J1 in the marketplace, so please come and say hi if you see me!

Save

All about Escher - Metamorphose Cowl

 

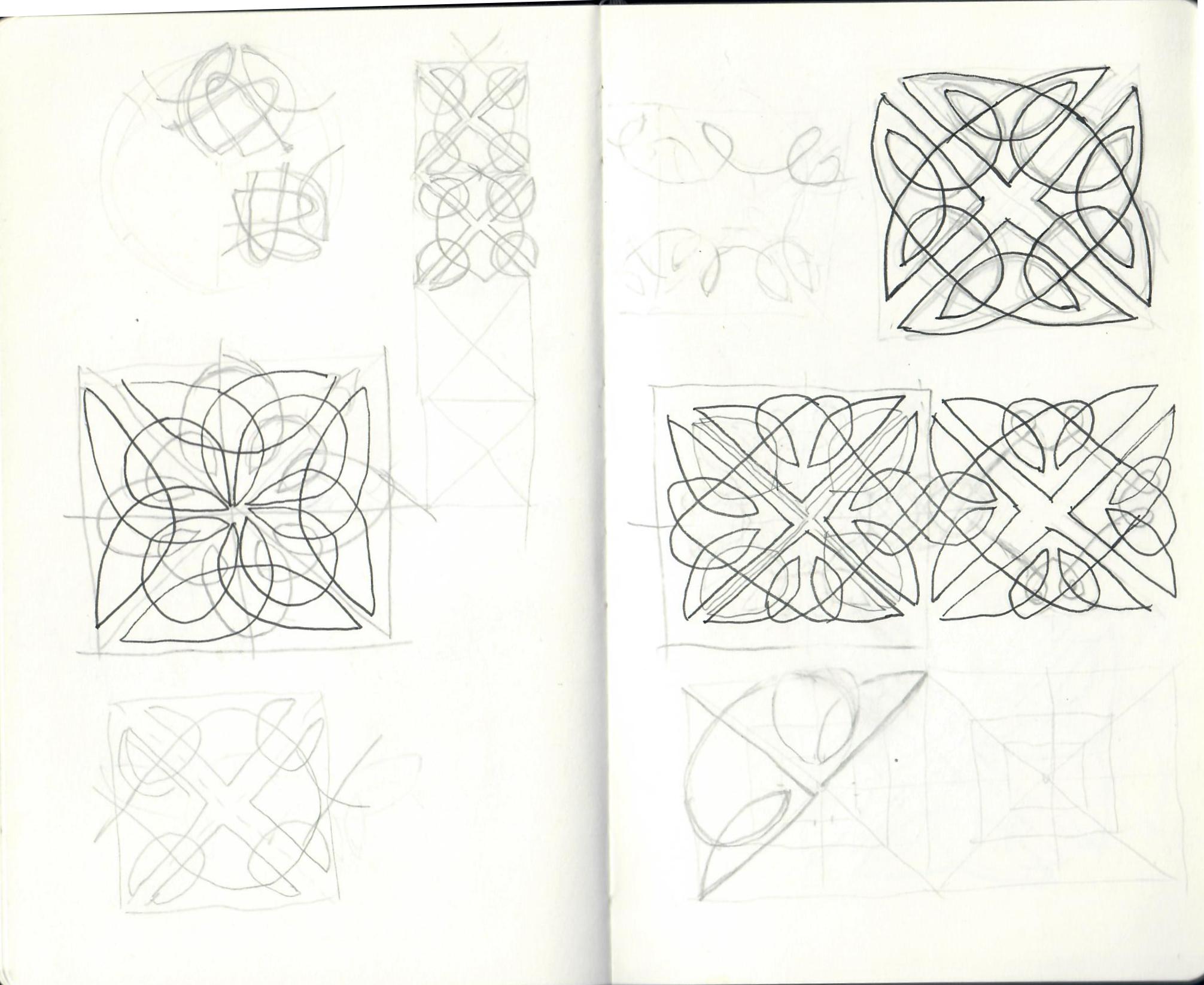
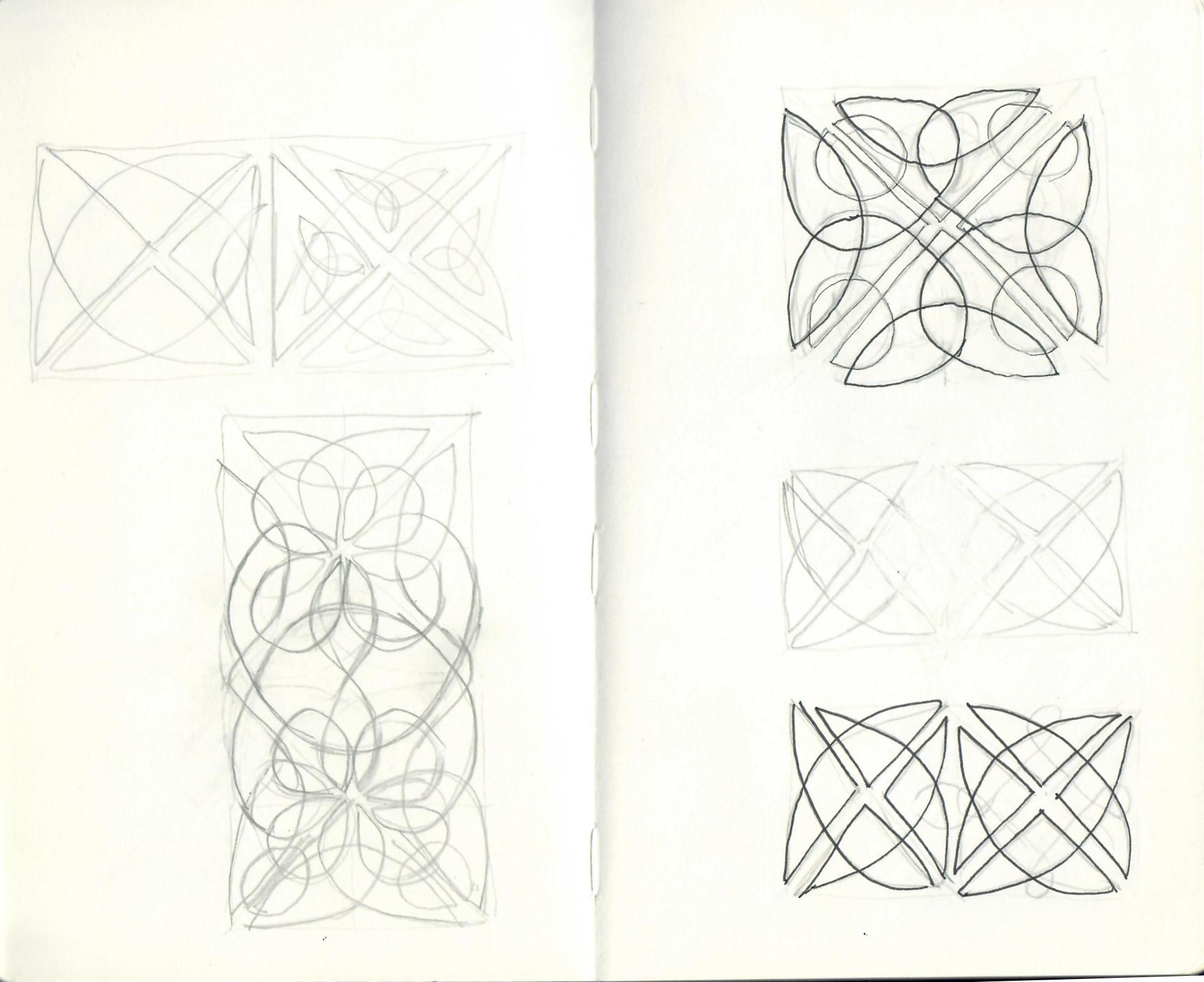
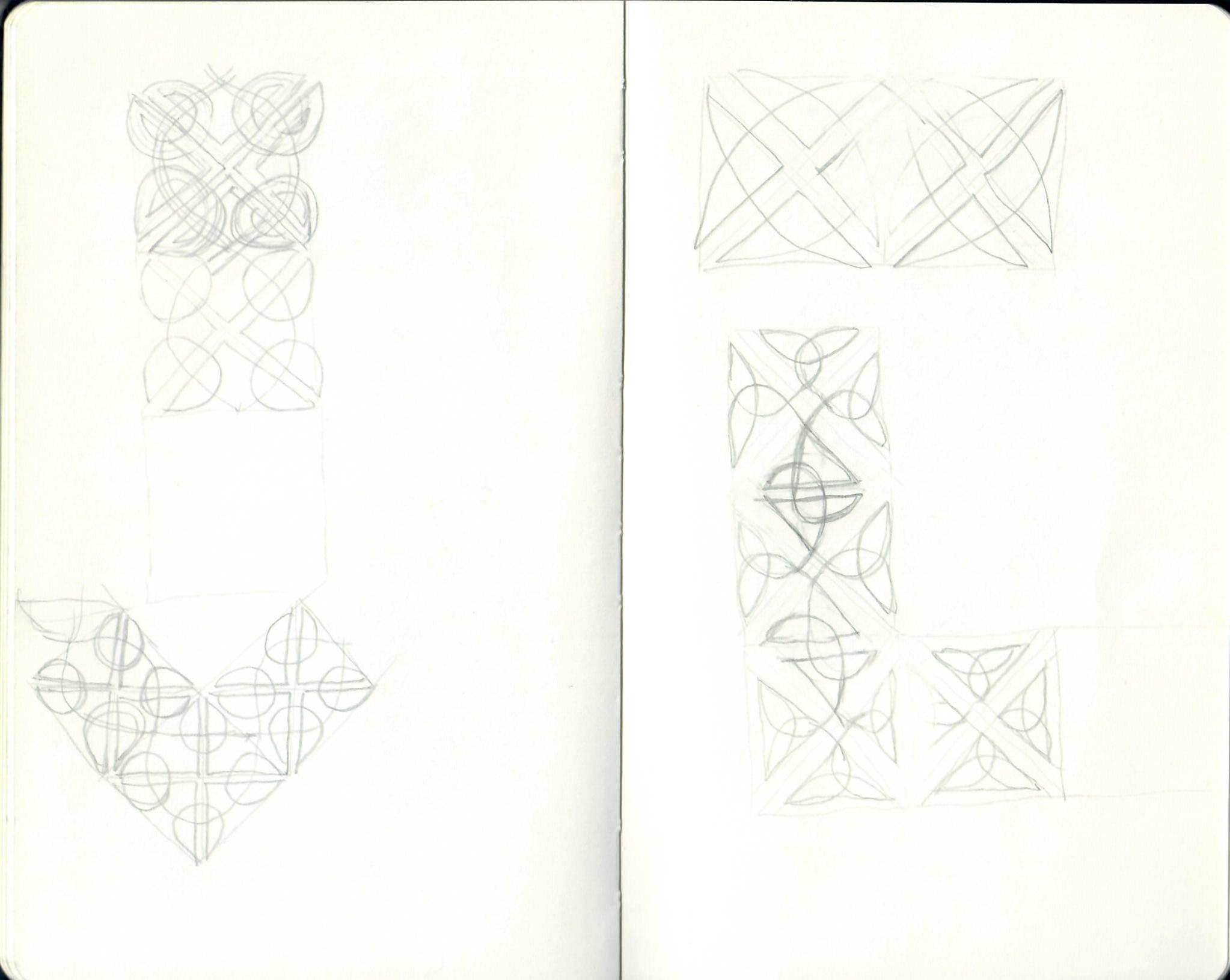
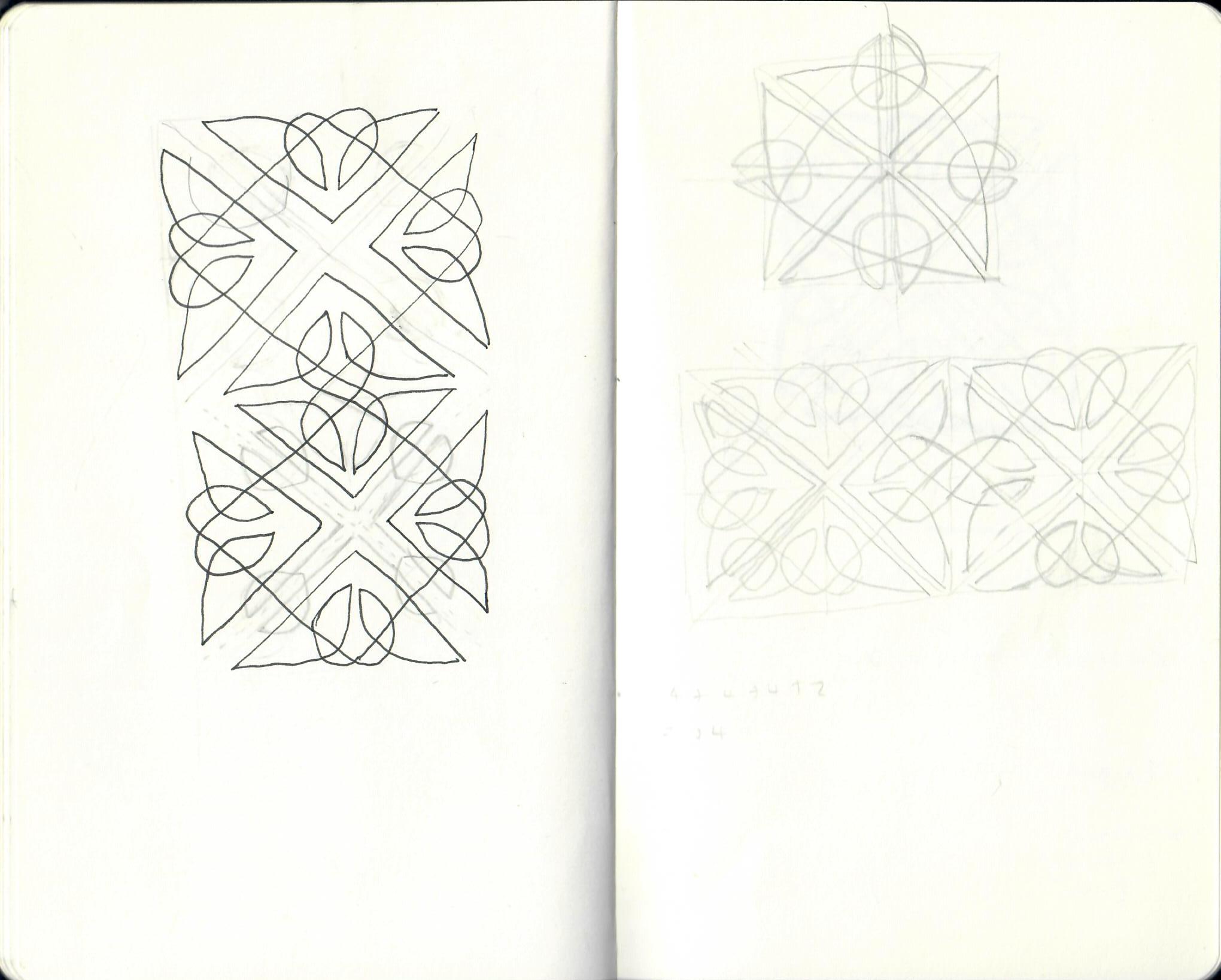
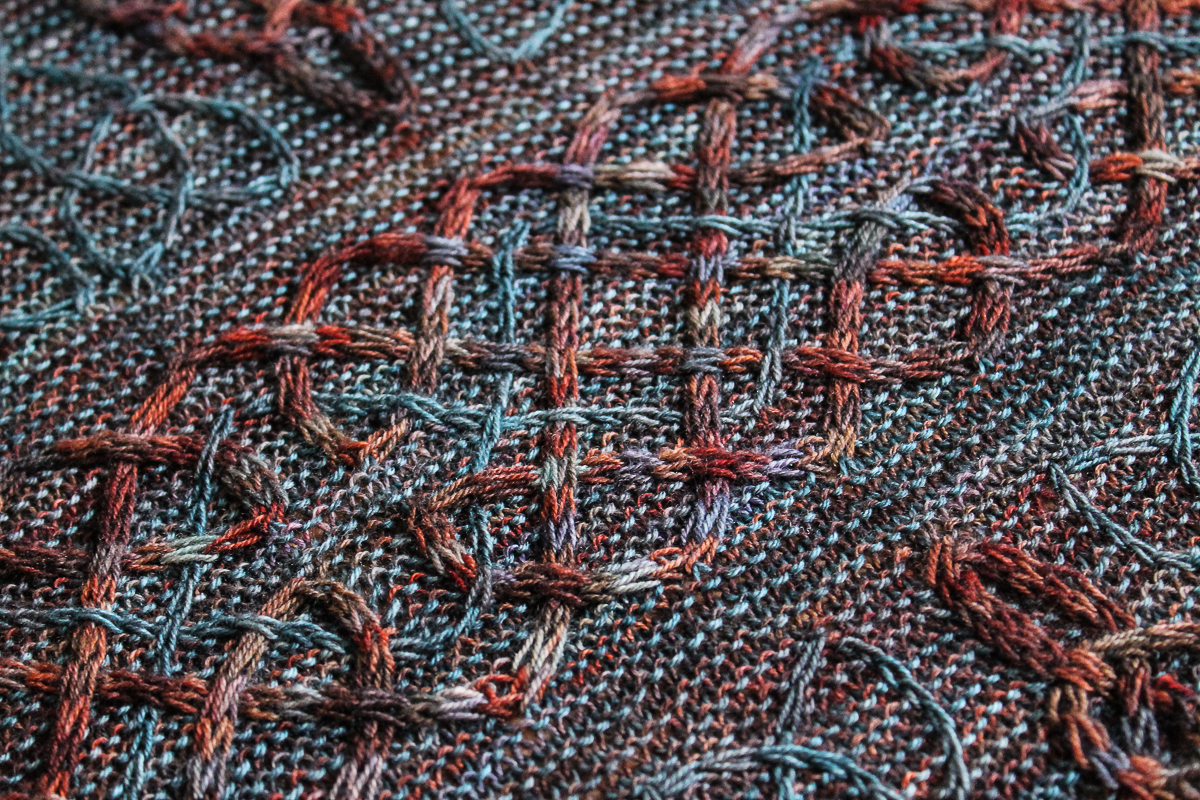When I was approached by Miss Babs to contribute a design to her 2016 Knitting Tour, and given the Netherlands as my country of inspiration, I knew instantly where to look for ideas: the work of the Dutch graphic artist Maurits Cornelis Escher.

I've loved M. C. Escher's work for as long as I can remember; possibly for longer than I was aware of his name, as he is one of those artists whose work is so distinctly unique (so much so that Escheresque exists as an adjective to describe artistic works derivative of his own) that its presence is still felt in popular culture (see, for example, the end scene of the 1986 film Labyrinth, inspired by Escher's Relativity); to the extent that, even if you've never heard of Escher, you would likely recognise one of his prints.

Escher is known for his artistic explorations of mathematical concepts such as impossible objects, infinity, perspective, and hyperbolic geometry, which he executed in finely detailed wood-cuts, lithographs and mezzotints.

I find Escher fascinating as an artist, and as a person, mainly because of his astonishing mathematical intuition (and his humble attitude towards it). He always played down his mathematical abilities, pointing out that he had never excelled in it as a subject at school, and had no love of algebra, yet somehow he frequently gravitated towards exploring mathematical subjects through visual means.(see this lecture from Oxford University for a fascinating look at Escher's intuitive grasp of these subjects).

Escher became obsessed with tessellations (which he referred to as 'regular divisions of the plane') after visiting the Alhambra and sketching the decorations there. When asked in 1951 about the symbolism in his print Day and Night, Escher replied:

"I think I have never yet done any work with the aim of symbolising a particular idea, but the fact that a symbol is sometimes discovered or remarked upon is valuable for me, because it makes it easier to accept the inexplicable nature of my hobbies, which constantly preoccupy me.

The regular division of the plane into congruent figures evoking an association in the observer with a familiar natural object is one of these hobbies or problems. This is really all there is to say about Day and Night. I have embarked on this geometric problem again and again over the years, trying to throw light on different aspects each time. I cannot imagine what my life would be like if this problem had never occurred to me; one might say that I am head over heels in love with it, and I still don't know why."

It's worth noting that Escher specifies here 'the regular division of the plane into congruent figures evoking an association in the observer with a familiar natural object', i.e. his obsession was not merely regular tessellation but involved finding tessellating shapes ('jigsaw pieces', as he referred to them sometimes) that evoked the shapes of familiar creatures or objects. Most often he played around with the shapes of birds, fish and reptiles, morphing in and out of negative space in increasingly complex ways, sometimes approaching infinity.

The sort of repeating patterns that are used to decorate fabric are, by their very nature, tessellations; indeed, all knitting stitch patterns are tessellations! When I began designing Metamorphose, I knew that I wanted to evoke that gradual morphing of shapes, emerging from negative space and almost becoming recognisable objects. I stopped short of trying to evoke an actual recognisable object, due to the complexity of knitting that this would involve! As always, when designing I'm trying to strike a balance between something that matches the idea in my mind, and is yet still enjoyable to knit without being too complicated. In this case, I sketched a basic morphing tessellation based on a triangle shape; reverse stocking stitch and seed stitch provide an alternating pattern (like the black and whites in Escher's prints).

The cowl/infinity scarf is worked as a seamless tube, with the ends grafted together with a twist, to form a Mobius-like loop. I feel like Escher would have been quite intrigued by the potential of knitted fabric to explore concepts like Mobius loops, tessellation and infinity. The way that the tessellating shapes repeat around the tube is very satisfying (albeit, a little tricky - some beginning-of-round marker shifts are necessary at points where the cables cross from one round to the next).

Delving into the world of Escher for inspiration for this design was great fun, and something I hope to return to in the future. I feel like there are a lot of possibilities for complex tessellating cable knitting, and I'd like to explore them.

Thanks to Miss Babs for inviting me on her Knitting Tour (and for the beautiful Killington yarn that she dyed in a special colourway for this design - fittingly named 'Escher').

Edited to add: if you're interested in learning more about M. C. Escher, this documentary is a great starting point.

Save

Lindisfarne shawl

Yesterday I was really pleased to finally be able to launch Lindisfarne, the second pattern in Illuminated Knits...

Lindisfarne is a large rectangular shawl, with an interesting construction. It's worked in the round, with a steek, then cut open at the end to produce fringed edges.

The shawl is worked from one side to the other, starting with a provisional cast-on and the edges are finished with an i-cord cast-off.

Like the first pattern in Illuminated Knits (the Iona blanket), this pattern makes extensive use of slipped-stitch cable colourwork. I've really fallen in love with this technique, because it makes it so easy to get the effects of colourwork without having to resort to stranded knitting or intarsia (having devoted so much time to working with cables and lace, I'm a woefully underdeveloped colourwork knitter, all fingers and thumbs!). I took the technique a bit further with this design, by incorporating cable patterns in both of the shades used to stripe the background. The heavier weight cables are in Malabrigo Sock Marte and the delicate twisted stitch cables are in Malabrigo Sock Persia.

In the central braid that runs down the length of the shawl, the twisted stitch cables wind in and out of the heavier cables. This is one of those marvellous knitting tricks that looks like it would involve fiddling around in a hopeless tangle with lots of balls of yarn at once - but magically, there is still only one strand of yarn being used on each round. I also managed to write the pattern in such a way that there are quite a few rest rounds - most of the cabling takes place on rounds where Marte is the main yarn, and the cables are worked for the twisted stitch cables by simply slipping them into position. On the next round, all that's required is to k tbl.

Above is a close-up of the fringe, after the steek has been cut and unravelled, blocked and then neatly knotted at regular intervals. I really love the effect of the two shades of yarn mingled together; it really gives the effect of a piece that has been woven, rather than knitted.

Another benefit of using slipped-stitch colourwork is that the back of the shawl looks really neat - just like striped garter stitch. There's something very satisfying about looking on the reverse side of a complex multi-coloured piece, and being surprised by the complete lack of floats!

As with the Iona blanket, this design was an absolute monster to design, plan, knit and write up - it was several months in the making and went through a lot of permutations before settling into its final form. Originally I had envisaged the shawl being covered in a repeating pattern of triangular knots, inspired by a knot from the Lindisfarne manuscript. It was quite late in the design process when I suddenly had the vision of the central braid, with the twisted stitch cables lacing in and out. I had to rewrite the design to fit it in, but I think it was worth it in the end!

Here's a few pics of the design in progress (note my utter inability to settle on a colour scheme!):